코딩테스트/programming_JAVA
[Java] baekjoon_1074 : Z
prometedor
2024. 1. 29. 18:22
분할 정복, 재귀
Z : Silver1
https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net




풀이
import java.io.*;
import java.util.*;
public class Main {
private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
// int size = (int) Math.pow(2, N);
int answer = recursiveZ(N, r, c, 0, 0);
bw.write(answer + "\n");
br.close();
bw.close();
}
public static int recursiveZ(int N, int r, int c, int startRow, int startCol) {
if (N == 0) {
return 0;
}
int halfSize = (int) Math.pow(2, N - 1);
int cellSize = (int) Math.pow(halfSize, 2);
if (r < startRow + halfSize && c < startCol + halfSize) {
return recursiveZ(N - 1, r, c, startRow, startCol);
} else if (r < startRow + halfSize && c >= startCol + halfSize) {
return cellSize + recursiveZ(N - 1, r, c, startRow, startCol + halfSize);
} else if (r >= startRow + halfSize && c < startCol + halfSize) {
return 2 * cellSize + recursiveZ(N - 1, r, c, startRow + halfSize, startCol);
} else {
return 3 * cellSize + recursiveZ(N - 1, r, c, startRow + halfSize, startCol + halfSize);
}
}
}
ㄴ 재귀적인 방법을 사용하여 Z모양으로 배열을 탐색하고, 특정한 위치인 (r, c) 가 몇 번째로 방문되는지를 찾아야 하는 문제다.
N = 2, r = 2, c = 1 일 경우를 그림으로 나타내면,
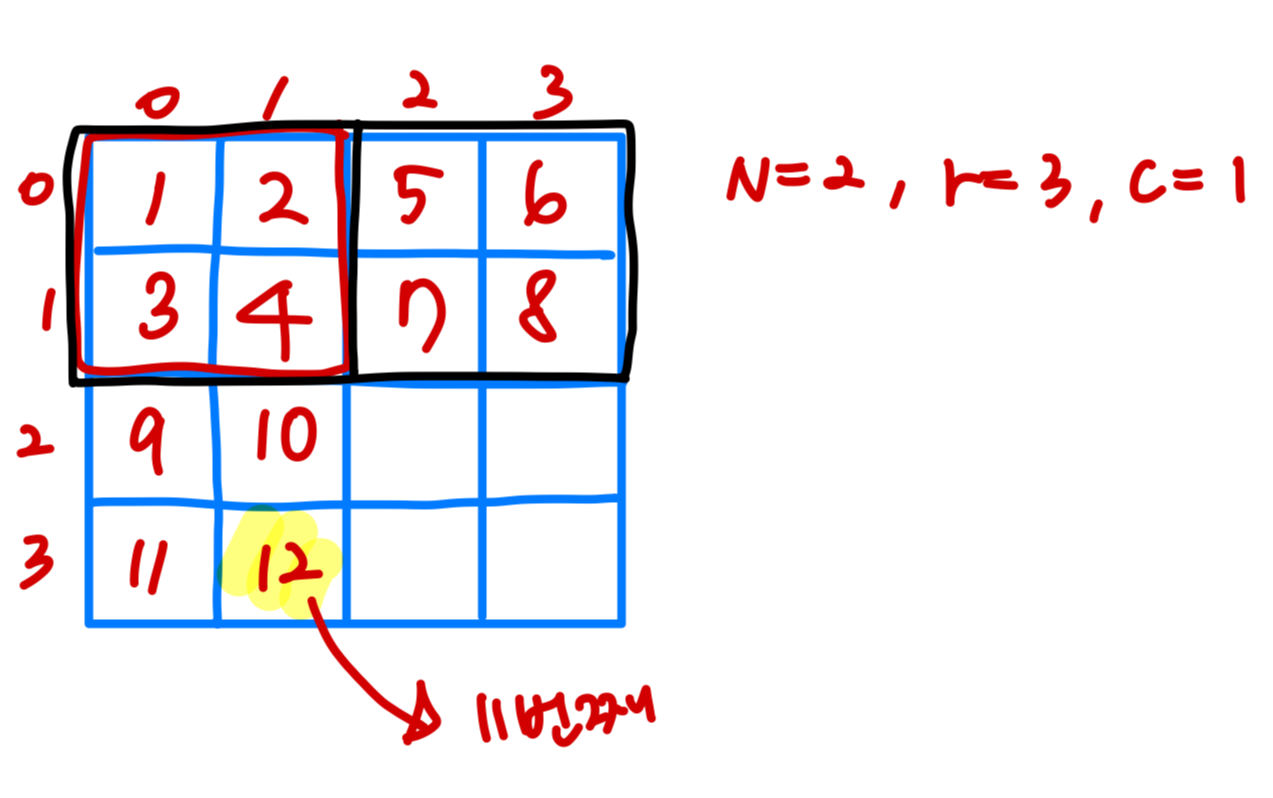
ㄴ 입력되는 크기 N에 따라 배열을 4등분하고,
ㄴ 각 등분된 배열을 다시 같은 과정을 반복하여 탐색하는 방식을 이용했다.
N은 배열의 크기를 나타내는 지수입니다. 2^N x 2^N 크기의 배열을 탐색한다.
r은 찾으려는 행의 인덱스이다.
c은 찾으려는 열의 인덱스이다.
startRow은 현재 배열 영역의 시작 행 인덱스이다.
startCol은 현재 배열 영역의 시작 열 인덱스이다.
ㄴ 함수 내부에서는 먼저 종료 조건을 검사하여, N이 0이면 탐색이 끝났음을 나타내고, 이때는 0을 반환한다.
ㄴ 그런 다음, 배열을 크기가 4등분하여 각각의 영역을 검사한다.
ㄴ 현재 배열의 크기가 2^N x 2^N이므로, 반으로 나눈 크기는 2^(N-1) x 2^(N-1)이다.
ㄴ 각각의 영역을 검사하여 (r, c)가 해당 영역에 속하는지 확인하고,
ㄴ 속하는 경우 해당 영역에서 재귀적으로 다시 recursiveZ 함수를 호출하도록 한다.
=> 호출 시에는 다음과 같이 인자를 전달한다.
- 왼쪽 위 영역 : (N - 1, r, c, startRow, startCol)
- 오른쪽 위 영역 : (N - 1, r, c, startRow, startCol + halfSize)
- 왼쪽 아래 영역 : (N - 1, r, c, startRow + halfSize, startCol)
- 오른쪽 아래 영역 : (N - 1, r, c, startRow + halfSize, startCol + halfSize)
여기서 각 영역의 크기는 halfSize로 계산되며, cellSize는 한 영역의 셀 개수이다.
이렇게 재귀적으로 호출하여 찾은 위치를 기준으로 해당 영역에 속한 값을 계산하고 반환하도록 했다.
