CNN(합성곱 신경망)
완전 연결 (Fully Connected) 신경망과 합성곱 (Convolution layer) 신경망

이미지 분석에서 완전연결(fully connected) 신경망의 문제점

ㄴ 데이터 형상의 무시 : 이미지 데이터를 1차원 벡터로 평탄화(flatten)하는 과정에서 공간 정보가 손실 되므로 이미지 내에서 픽셀들 간의 상대적인 위치 정보가 무시됨
ㄴ 변수의 개수 : 매개변수(parameter)의 수가 매우 많아지고, 모델의 복잡도가 높아지는 경향이 있으며 이는 과적합(overfitting)의 문제를 유발할 수 있음
ㄴ 네트워크 크기 : 입력 이미지의 모든 픽셀이 출력층에 직접 연결되는데, 입력 이미지의 크기가 커지면 모델 파라미터의 수도 비례해서 증가하게 되어 과적합과 계산 비용 증가 등의 문제를 유발함
ㄴ 학습 시간의 문제 : 모든 뉴런이 연결되어 있으므로, 연산량이 매우 크고 병목 현상이 발생할 가능성이 높음
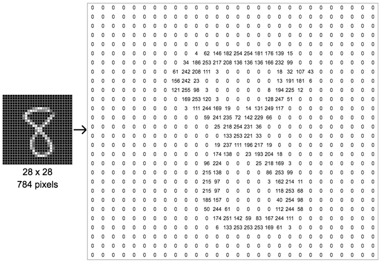
ㄴ 위 손글씨 데이터는 높이가 28, 너비가 28인 흑백 이미지므로 채널 수가 1임을 고려하면 (28 × 28 × 1)의 크기를 가지는 3차원 텐서임
= > 이미지 데이터의 경우 3차원(세로, 가로, 채널)의 형상을 가지며, 공간적 구조(spatial structure)를 지님

ㄴ 높이가 28, 너비가 28인 컬러 이미지는 적색(Red), 녹색(Green), 청색(Blue) 채널 수가 3개임을 고려하면 이 이미지의 텐서는 (28 × 28 × 3)의 크기를 가지는 3차원 텐서
= > 공간적으로 가까운 픽셀은 보통 시각적으로 유사한 패턴을 가지며, RGB의 각 채널은 서로 상호 연관되어 있음
합성곱층 (Convolutional Layer, Conv Layer)

ㄴ 이미지 데이터는 일반적으로 채널, 세로, 가로 이렇게 3차원으로 구성된 데이터
ㄴ 합성곱에서는 3차원 데이터(1, 28, 28)를 입력하고 3차원의 데이터로 출력하므로 형상을 유지 가능
(3차원의 이미지 그대로 입력층에 입력받으며, 출력 또한 3차원 데이터로 출력하여 다음 계층(layer)으로 전달)
ㄴ CNN에서는 이러한 입출력 데이터를 특징맵(Feautre Map)이라고 함
ㄴ 합성곱층 뉴런의 수용영역(receptive field)안에 있는 픽셀에만 연결
ㄴ 앞의 합성곱층에서는 저수준 특성에 집중하고, 그 다음 합성곱층에서는 고수준 특성으로 조합
필터 (Filter)

ㄴ 필터가 합성곱층에서의 가중치 파라미터(W)에 해당함
ㄴ 학습단계에서 적절한 필터를 찾도록 학습
ㄴ 입력데이터에 필터를 적용하여 필터와 유사한 이미지의 영역을 강조하는 특성맵(feature map)을 출력
하여 다음 층(layer)으로 전달
합성곱 연산(Convolution operation)
** 커널(kernel)은 일반적으로 3 × 3 또는 5 × 5를 사용

ㄴ (1×1) + (2×0) + (3×1) + (2×1) + (1×0) + (0×1) + (3×0) + (0×1) + (1×0) = 6

ㄴ (2×1) + (3×0) + (4×1) + (1×1) + (0×0) + (1×1) + (0×0) + (1×1) + (1×0) = 9

ㄴ (3×1) + (4×0) + (5×1) + (0×1) + (1×0) + (2×1) + (1×0) + (1×1) + (0×0) = 11
=> 이렇게 해서 마지막 9번째 값 까지 모두 합성곱 연산을 한 결과를 특성맵(feature map) 이라고 함
위 그림에서는 커널의 크기가 3 x 3 이었지만, 커널의 크기는 사용자가 정할 수 있음
또한 커널의 이동 범위가 위의 예제에서는 한 칸 이었지만, 이 또한 사용자가 정할 수 있음
여기서 이 이동 범위를 스트라이드(stride) 라고 함
스트라이드(stride)
ㄴ 필터가 이동할 간격
ㄴ 출력 데이터의 크기를 조절하기 위해 사용
ㄴ 보통 1과 같이 작은 값이 작동이 더 잘 됨

ㄴ filter 가 1칸씩 이동하는 간격을 스트라이드(stride)라고 하므로 위 그림은 스트라이드(stride)가 1임

ㄴ filter 가 1칸씩 이동하는 간격을 스트라이드(stride)라고 하므로 위 그림은 스트라이드(stride)가 1임
= > 이렇게 filter가 이동하다 보면 마지막이 딱 맞지 않는 경우 (e.g. 4 x 4 input에 3×3 filter가 2 stride만큼 이동)에는 padding을 추가하여 길이를 맞춤
= > 이때 padding 값은 보통 0으로 채움
패딩

ㄴ 합성곱 연산을 수행하기 전, 입력데이터 주변을 특정값으로 채워 늘리는 것
ㄴ 주로 zero-padding을 사용
ㄴ 데이터의 크기는 Conv Layer를 지날 때 마다 작아지므로 가장자리 정보가 사라지는 문제 발생하기 때문에 패딩을 사용
ㄴ 합성곱 계층의 출력이 입력 데이터의 공간적 크기와 동일하게 맞춰주기 위해 사용
3차원 데이터의 합성곱

ㄴ 입력의 채널 수와 필터의 채널 수가 같아야 함
= > 위 그림에서 입력의 채널수와 필터의 채널 수는 모두 3으로 같음
풀링층(Pooling layer)
ㄴ 그림의 사이즈를 점진적으로 줄이는 법
ㄴ Max-Pooling, Average Pooling
ㄴ Max-Pooling : 해당영역에서 최대값을 찾는 방법
ㄴ Average Pooling : 해당영역에서 평균값을 계산하는 방법

ㄴ 2 x 2 filter로 2 stride를 적용하여 4x4 이미지를 2x2이미지로 변환
CNN 모델 및 코드
Dense, Conv2D, Flatten
from keras.models import Sequential
from keras.layers import Dense, Conv2D, Flatten
model = Sequential()
# model.add(Dense(units=10, input_shape(3,)))
model.add(Conv2D(filters=10, kernel_size=(3, 3), # kernal_size 는 이미지를 자르는 규격을 의미
input_shape=(8, 8, 1))) # (rows, rows, channels)의 형태 --> channels 의 1 : 흑백 / 3 : 컬러
model.add(Conv2D(7, (2, 2), activation='relu'))
model.add(Flatten())
model.add(Dense(32, activation='relu'))
model.add(Dense(10, activation='softmax'))ㄴ Dense : 전결합층(fully connected layer)으로, 모든 입력 노드가 모든 출력 노드와 연결되어 있는 신경망 계층
= > 입력값에 가중치와 편향을 더한 후, 활성화 함수를 적용하여 출력값을 계산
ㄴ Conv2D : 2D 합성곱 신경망 계층으로, 이미지와 같은 2차원 데이터에서 특징을 추출하기 위해 사용
= > 필터(kernel)를 사용하여 입력 이미지를 스캔하고, 지정된 수의 출력 채널을 생성
ㄴ Flatten : 다차원 배열을 1차원으로 변환
= > Conv2D와 같은 2D 레이어 다음에 사용
= > 입력값을 1차원 벡터로 변환하여 Dense 레이어와 같은 전결합층에서 처리하기 쉽게 만들어 줌
MaxPooling2D
from keras.models import Sequential
from keras.layers import Dense, Conv2D, Flatten, MaxPooling2D
model = Sequential()
model.add(Conv2D(filters=64, kernel_size=(3, 3), # kernal_size 는 이미지를 자르는 규격을 의미
padding='same',
input_shape=(28, 28, 1))) # (rows, rows, channels)의 형태 --> channels 의 1 : 흑백 / 3 : 컬러
model.add(MaxPooling2D())
model.add(Conv2D(32, (2, 2),
padding='valid',
activation='relu'))
model.add(Flatten())
model.add(Dense(32, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(10, activation='softmax'))ㄴ MaxPooling2D :
= > 이미지의 국부적인 특징을 추출하고, 최종적으로 전체 이미지를 분류하는데 사용
= > 이미지에서 특징 맵(feature map)을 다운샘플링하여 크기를 줄이는 역할을 함
= > 주로 이미지 인식과 관련된 문제에서 사용
= > 입력 데이터의 크기를 줄이고, 불필요한 특징을 제거하여 계산 복잡도를 줄일 수 있음
'네이버클라우드 > AI' 카테고리의 다른 글
| AI 5일차 (2023-05-12) 인공지능 기초 - 자연어처리(NLP) 기초 (0) | 2023.05.12 |
|---|---|
| AI 4일차 (2023-05-11) 인공지능 기초 - 이미지 분석 : 데이터 셋 (0) | 2023.05.11 |
| AI 3일차 (2023-05-10) 인공지능 기초 - Save model, Save weight, Model Check Point (0) | 2023.05.10 |
| AI 3일차 (2023-05-10) 인공지능 기초 - Validation split, 과적합(Overfitting)과 Early Stopping (0) | 2023.05.10 |
| AI 3일차 (2023-05-10) 인공지능 기초 - Optimizer (0) | 2023.05.10 |



